Euclidea 游戏解答与证明

在 X Round 4 上做到了「尺规作图」这道非常有意思的提交答案题，后来得知这题的灵感来自于 Euclidea 这款智力游戏，于是决定体验一下。

然后就意识到自己的几何水平退化实在太厉害了…于是决定写篇博客来记录一下自己解题的心路历程。

1. Alpha

1.1 Angle of 60°

给出一条射线，作出以该射线为边的 $60^\circ$ 角。

解法

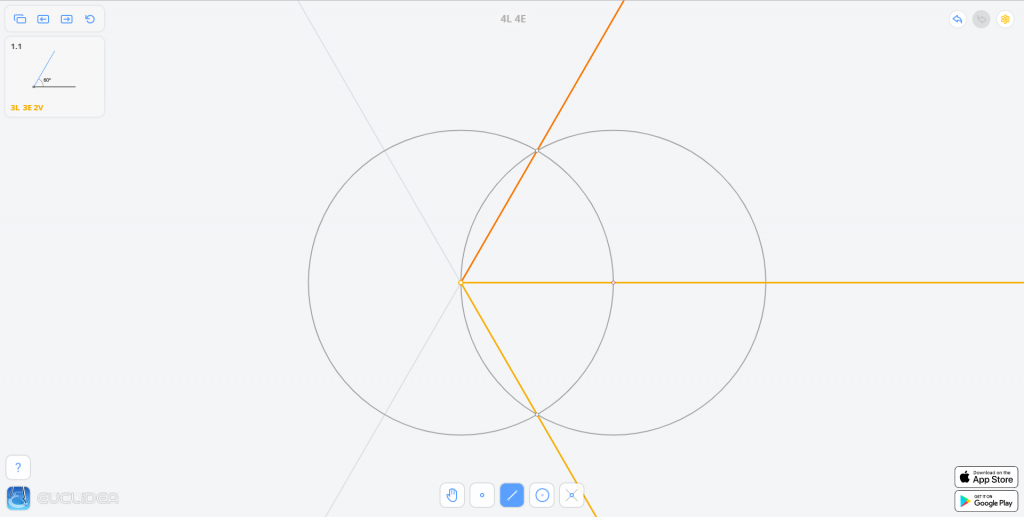
为了方便，设射线的端点为 $O$，我们在射线上取一点 $A$。

分别以 $O$ 和 $A$ 为圆心，$OA$ 为半径画圆，两圆交于 $C_1,C_2$ 两点。

则 $\angle C_1OA$ 和 $\angle C_2OA$ 即为所求角（别忘了把这两个角都画出来，从而解锁隐藏 V 星）。

花费：3L 3E（只画出一个角）。

附最终完成图（图简单就不标点了）：

1.2 Perpendicular Bisector

作出给定线段的中垂线。

解法

初中几何经典作图题。

步骤如下：

1. 以两端点为圆心，线段长度为半径，作两个圆，交于 $C_1,C_2$ 两点；
2. 连接 $C_1C_2$ 即为所求。

附中垂线的判定：若一点到线段两端点的距离相等，则该点在线段的中垂线上。

结合这个定义就不难理解这个作图方式的正确性了。

花费：3L 3E。

1.3 Midpoint

给出两定点，作两定点连线段的中点。

解法

连接两点后，直接用中垂线工具作出线段中垂线，与线段交点即为所求。

花费：2L 4E。

图略。

1.4 Circle in Square

作给定正方形的内接圆。

解法

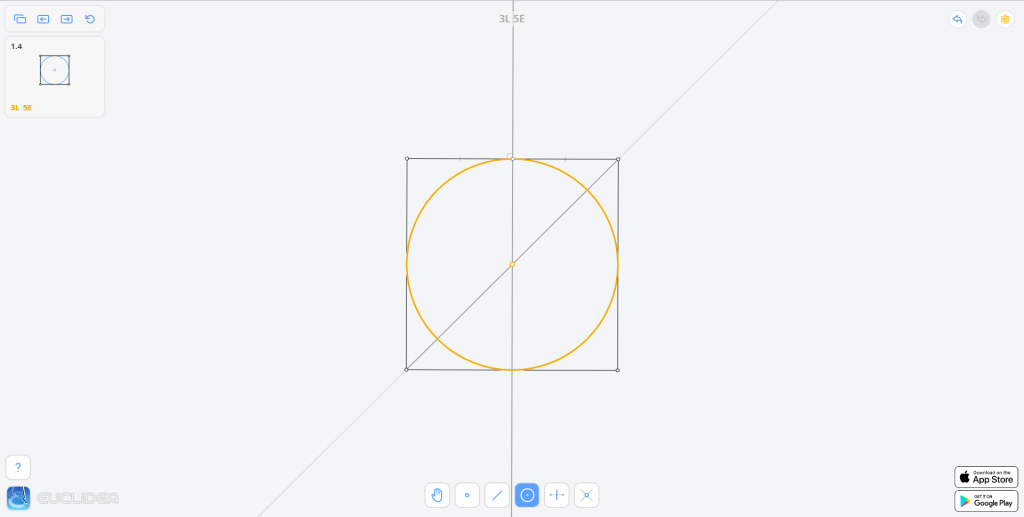
1. 连接一条对角线；
2. 作其中一条边的中垂线，交该边于 $P$ 点，交对角线于 $O$ 点。
3. 以 $O$ 点为圆心，$OP$ 为半径作圆，即为所求。

花费：3L 5E。

1.5 Rhombus in Rectangle

在给出的矩形内，作一个菱形，要求菱形和矩形共用一条对角线。

解法

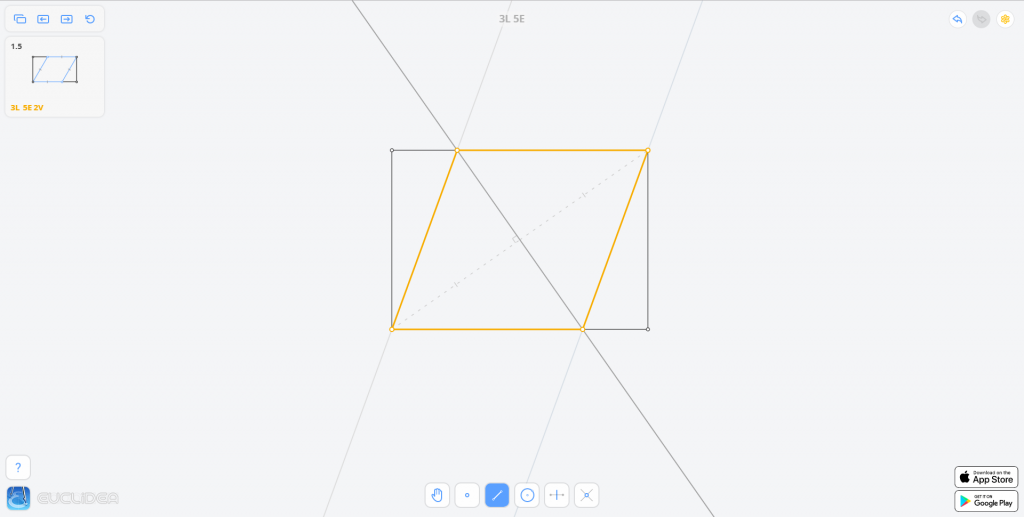
关于菱形的对角线，有一个重要性质：菱形的两条对角线互相垂直平分。

矩形的一条对角线作为菱形的一条对角线，菱形的另一条对角线可以利用上述性质，作出矩形对角线的中垂线得到。

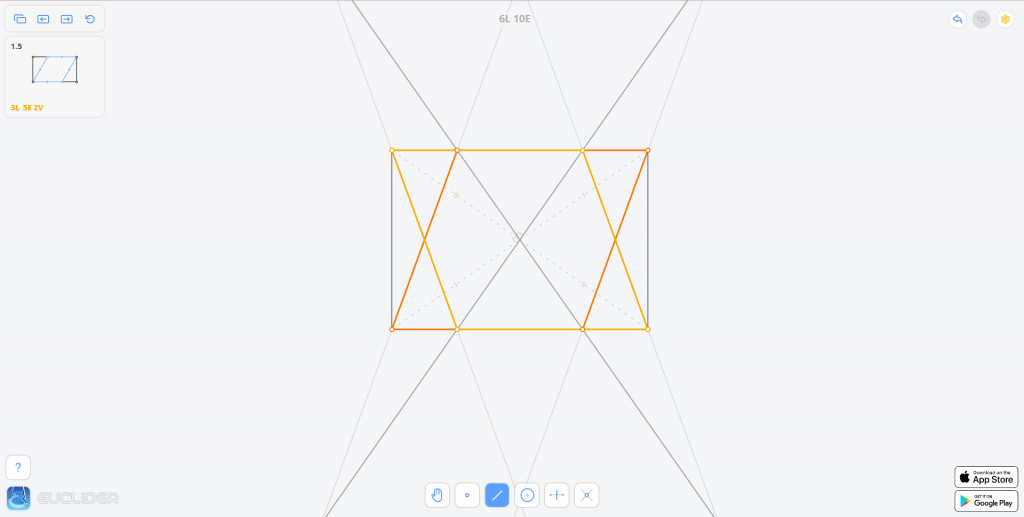
因为矩形有两条对角线，我们可以用两条对角线分别画出两个满足题意的菱形。

花费：3L 5E（只画出一个菱形）。

1.6 Circle Center

求出给定圆的圆心。

解法一

在圆上任取两点，作两点连线的中垂线，由垂径定理可知这条中垂线为圆的直径，作该中垂线的中垂线，交点即为圆心。

花费：2L 6E。

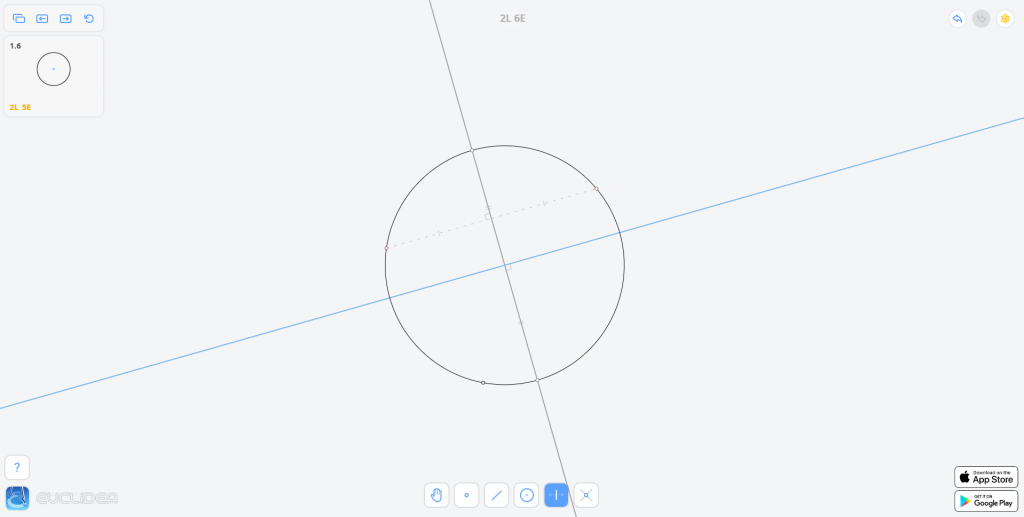
解法二

上面的做法满足了 L 的要求，但没有满足 E 的要求。而下面的做法恰恰相反，只满足了 E 的要求。这意味着我们需要完成这关两次才能拿到三星的成绩。

先在圆上取一点，记为 $A$，以 $A$ 为圆心，小于给出圆直径的长度为半径 $r$ 作圆 $C_1$。

$C_1$ 与给出的圆会产生两个交点，记其中一个交点为 $B$。接下来以 $B$ 为圆心，$AB$ 长为半径（因为 $B$ 在 $C_1$ 上，所以 $|AB|=r$）作圆 $C_2$。

$C_2$ 与给出的圆会产生两个交点，其中一个交点为 $A$，另外一个交点我们记为 $C$。接下来以 $C$ 为圆心，$BC$ 长为半径（和上面同理，$|BC|=r$）作圆 $C_3$。

$C_1$ 和 $C_2$ 会产生两个交点，记作 $D_1,D_2$。 $C_2$ 和 $C_3$ 会产生两个交点，记作 $E_1,E_2$。

连接 $D_1D_2$ 和 $E_1E_2$ 并延长，两直线交点即为所求圆心。

结合下图理解一下：

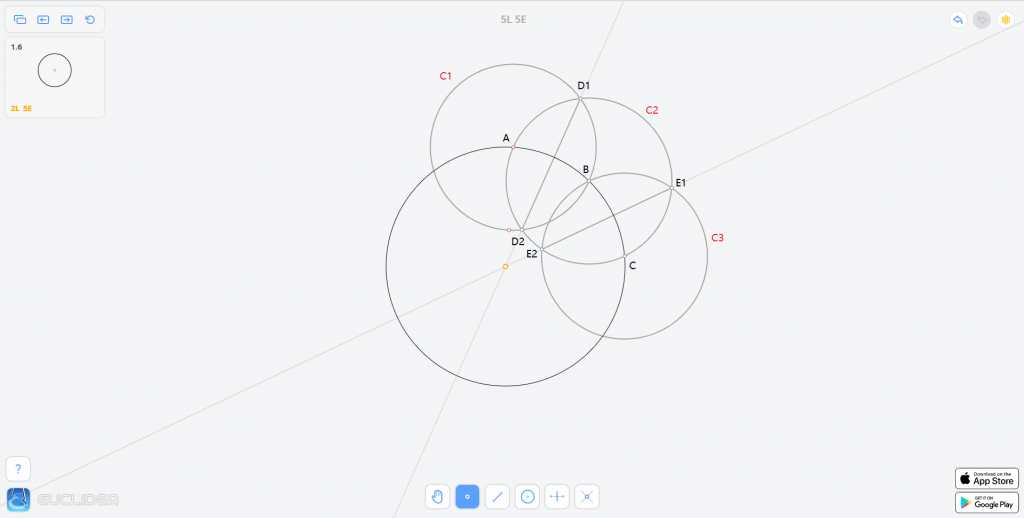
为什么这样是正确的呢？

$D_1,D_2$ 到 $A$ 点和 $B$ 点的距离相等，因此 $D_1D_2$ 为 $AB$ 的中垂线。

而根据垂径定理，$D_1D_2$ 一定经过圆心。

同理 $E_1E_2$ 是 $BC$ 的中垂线，且也过圆心。

因而这两条直线的交点即为圆心。

花费：5L 5E。

1.7 Inscribed Square

给出圆的圆心，求其内接正方形。正方形的一个顶点已经给出。

解法一

正方形两条对角线互相垂直平分，根据这一性质可以画出两条对角线，从而确定四个顶点。将这几个顶点顺次连接即可。

花费：6L 8E

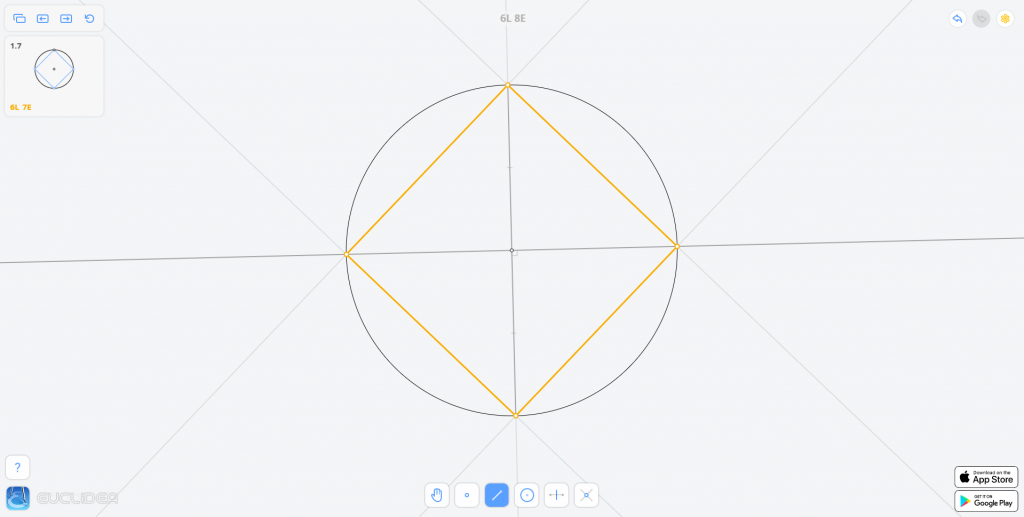
解法二

我们设给定圆的圆心为 $O$。

按以下步骤来作图：

1. 在圆上取一点 $A$，以 $A$ 为圆心，$AO$ 长为半径作圆 $C_1$，交给定圆于 $B,C$ 两点。
2. 以 $B$ 为圆心，$BC$ 长为半径作圆 $C_2$，交给定圆于 $D$ 点。

先附一张图：

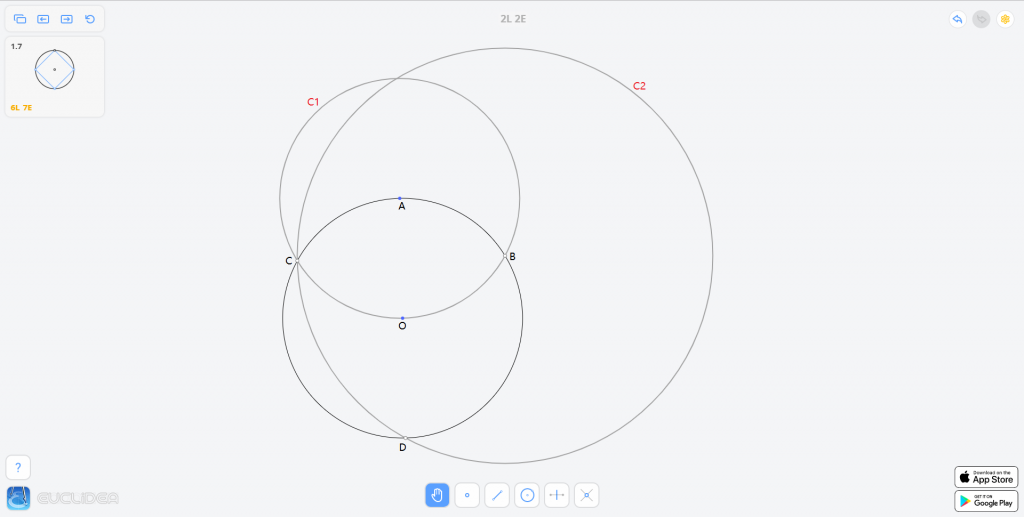
接下来，连接 $BO$ 并延长，交 $C_2$ 于 $E,F$ 两点，连接 $DE$ 并延长，交给定圆于 $G$ 点。

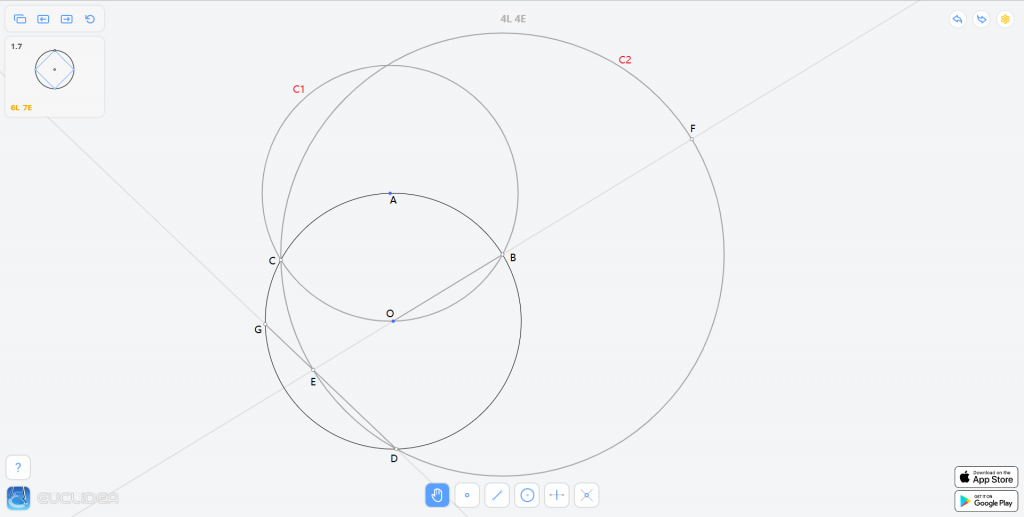
连接 $DF$ 交给定圆于 $H$，连接 $AG,AH$，则四边形 $AHDG$ 即为所求正方形。

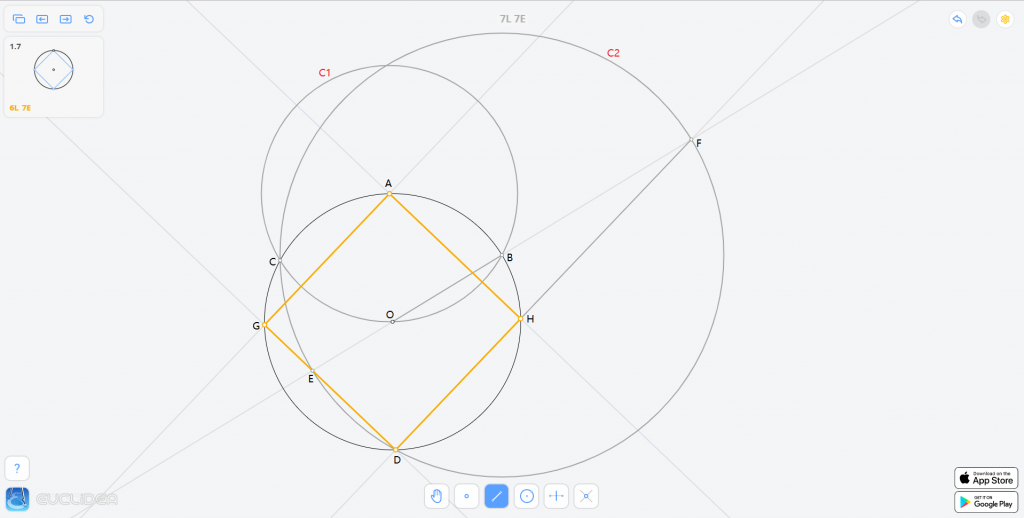
正确性证明待填坑。

2. Beta

2.1 Angle Bisector

作已知角的平分线。

解法一

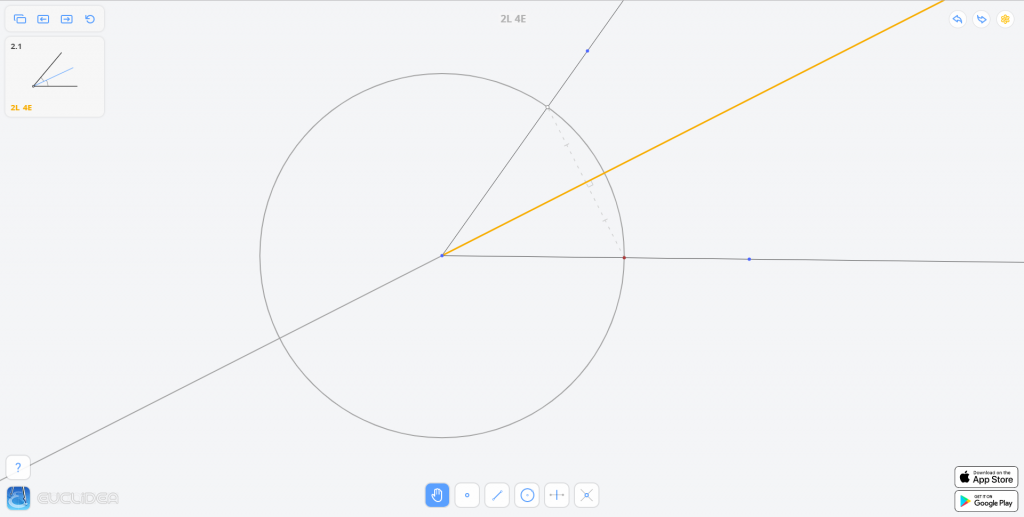
在一边上任取一点 $A$，以顶点 $O$ 为圆心，$OA$ 为半径作圆，交另外一边于 $B$。

作 $AB$ 的中垂线即为所求。

根据等腰三角形三线合一的性质容易证明这一作法是正确的。

花费：2L 4E

2.2 Intersection of Angle Bisectors

求给定三角形的内心（三条角平分线的交点，三角形内切圆圆心）。

解法一

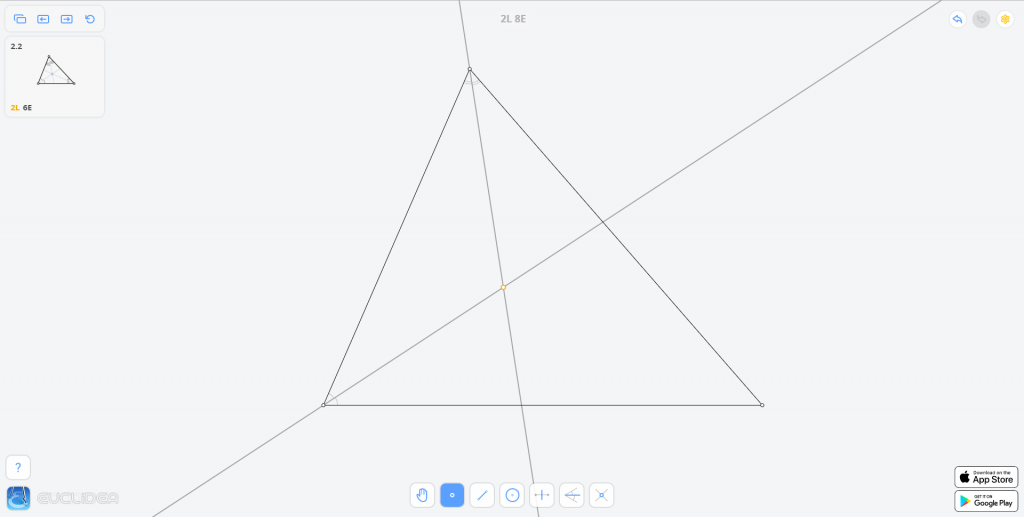
直接用角平分线工具画出两条角平分线，交点即为所求。

花费：2L 8E

解法二

用传统的方式画角平分线，作图的时候重复利用已有的圆即可减小开销。

（待填坑）

2.3 Angle of 30°

给出一条射线，作出以该射线为边的 $30^\circ$ 角。

解法一

基于 1.1 的做法先作出 $60^\circ$ 角，然后作角平分线即可。

花费：3L 6E（作出一个角）

解法二

2.4 Double Angle

给出一个已知角，构造一个角与之相等，且该角与已知角共用一条边。

解法

考虑构造全等三角形。

3.5 Circle through Point Tangent to Line

给出直线外一点 A 和直线上一点 B，构造一个圆，使其过 A 点，且与直线在 B 点相切。

解法一

利用 B 点是切点这一条件，过 B 作切线的垂线，则圆心一定在该垂线上。

然后利用垂径定理作 AB 的垂直平分线，与切线的垂线交点即圆心。

花费：3L 7E。