感觉这次题目算法性似乎很强,很多题目都是结论题,思维难度也不算太高,这里给出题人点个赞。(滑稽)
题目链接
https://codeforces.com/contest/1064
A. Make a triangle!
大意
给出长度分别为 \(a , b , c\) 的三根木棒,求出至少将木棒延长多长可以使这三根木棒拼成一个三角形。
题解
这里设 \(a \leq b \leq c\),毫无悬念,当 \(a+b>c\) 时,答案为 \(0\)。
否则,我们可以延长最短的那根木棒,使得 \(a+b>c\) 成立。这时的答案为 \(c-(a+b+1)\)。
#include <cstdio>
#include <algorithm>
using namespace std;
int a[3];
int main()
{
scanf("%d%d%d",&a[0],&a[1],&a[2]);
sort(a,a+3);
if(a[0]+a[1]>a[2])printf("0\n");
else printf("%d\n",a[2]-(a[0]+a[1])+1);
return 0;
}
B. Equations of Mathematical Magic
大意
给出 \(a\),判断方程 \(a-(a \oplus x)-x=0\) 的解的个数。
题解
移项后可得 \(a \oplus x=a-x\),随便找几个规律就会知道, \(x\) 是方程的解当且仅当 \(x\) 的二进制表示中的 \(1\) 是 \(a\) 中 \(1\) 的子集。
举个栗子,当 \(a=13 ((1101)_2)\) 时,\(x=4 ((0100)_2)\) 就是方程的一个根。
根据子集的规律可知,假如 \(a\) 中有 \(x\) 位的值为 \(1\),答案就是 \(2^x\)。
#include <stdio.h>
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int a;
scanf("%d",&a);
if(a==0)puts("1");
else
{
int cnt=1;
while(a!=0)
{
if(a%2)cnt*=2;
a>>=1;
}
printf("%d\n",cnt);
}
}
return 0;
}
C. Oh Those Palindromes
大意
给出一个字符串,通过重新排序,使得新字符串的回文子串数目最多。
题解
“abccba”和”aabbcc”哪个回文子串多?答案事实上是一样多的。(都是 \(9\) 个)
所以似乎可以猜一个结论:直接把字符串按字母顺序排列不就好了?(这个结论事实上是正确的)
#include <cstdio>
#include <algorithm>
using namespace std;
char s[100005];
int main()
{
int n;
scanf("%d",&n);
scanf("%s",s);
sort(s,s+n);
printf("%s",s);
return 0;
}
E. Dwarves, Hats and Extrasensory Abilities
大意
这是一道交互题。
你的程序将读入一个数字 \(n\),每次你输出一个位于第一象限内的点 \((x,y)\),交互器将会给出该点的颜色(”black”或”white”)。当你输出 \(n\) 个点后,你应该输出两个点 \((x1,y1),(x2,y2)\),这两个点连成的直线将把整个平面分成两侧,位于直线同一侧的点应该颜色相同,并且你输出的任何一个点都不应刚好在这条直线上。
题解
刚开始误解了题意,于是瞎搞了一个程序:
#include <stdio.h>
int a[35];
char s[35];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
printf("%d %d\n",0,(i-1)*2);
fflush(stdout);
scanf("%s",s);
if(s[0]=='b')a[i]=1;
else a[i]=0;
}
int y=2*n;
for(int i=2;i<=n;i++)
if(a[i]!=a[i-1])
{
y=(i-1)*2-1;
break;
}
printf("%d %d %d %d",0,y,1,y);
return 0;
}
题目中说到交互器具有“自适应性”,然而被误解成对于我们给出的输出,交互器一定会保证存在一种合法的分割方案,结果死的很惨。
那么我们就不能把所有点都放在一条直线上了?其实还是可以的。
事实上,我们可以采用二分的方法来放点。
首先在原点上放一个点,然后在数轴的中点放一个点(对于本题,这个点可以放在 \((5 * 10 ^ 8,0)\) 这个位置上),然后每次都在两端点颜色不相同的区间的中点上继续放点,直到点放完为止。最后的答案就位于相邻的黑点和白点之间。
听起来有些绕?放个图来加深一下理解:
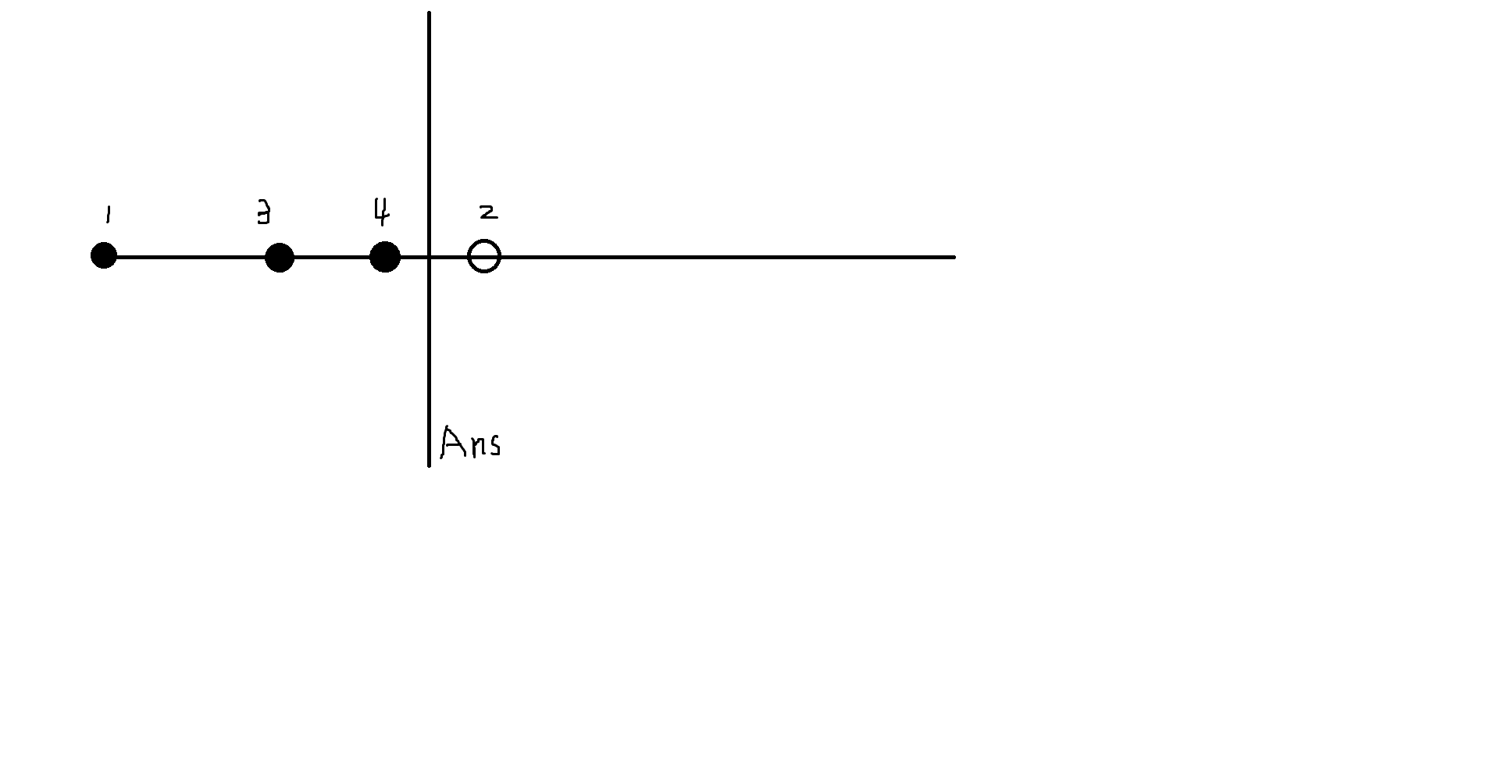
这样放点就确保了黑点白点被隔开的情况不会发生了。