目录
显示
题目链接
https://loj.ac/problem/3279(loj 暂不支持通信题,所以这道题还没公开)
题解
Subtask 4
当 \(A \geq 3\) 时,我们可以 BFS 遍历整张图,将图上的点按距离分层。
显然图上的边只有两种类型:层内边和层间边。
对于连接第 \(d\) 层和第 \(d+1\) 层的层间边,这条边的颜色可以设为 \(d \bmod 3\);对于第 \(d\) 层的层内边,边的颜色可以设为 \(d \bmod 3\)。
这样对于每一个点,我们都可以分辨出深度严格递减的方向,按照这个方向走即可。
期望得分:15 pts。
Subtask 7
只有两种颜色了,不过好消息是这种情况下我们只需解决树的问题。
如果一个点的度数大于等于 \(3\),显然颜色仅出现一次的边就是深度减小的方向。
如果一个点的度数为 \(2\),按照之前的染色方式肯定行不通,因为我们无法分清楚哪个方向是深度减小的方向。
步数限制是 \(d+6\) 步,这意味着我们最多往深度增大的方向走 \(3\) 步。
考虑按照这种方案染色(图借用了官方题解的图):
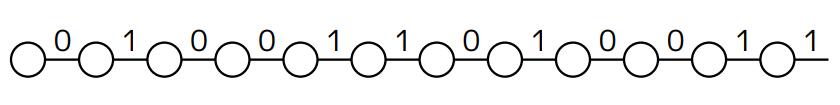
易知无论我们最开始处在链上的哪个点,我们最多向深度增大的方向走三步就可以意识到方向错误(具体讨论过程略,详见代码实现)。
且一旦我们确定了正确的方向,我们只需一直朝这个方向走即可,不用回头,从而可以将步数上限控制在 \(d+6\) 步。
期望得分:100 pts。
Anthony.cpp:
#include "Anthony.h"
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int,int> pii;
vector<pii> e[20005];
int dis[20005],fac[20005];
namespace col01
{
vector<int> res;
const int col[]={0,1,0,0,1,1};
void dfs(int u,int fa,int p)
{
for(auto E:e[u])
{
int v=E.first,id=E.second;
if(v==fa)continue;
res[id]=col[p];
if(e[v].size()>2)
dfs(v,u,!col[p]);
else
dfs(v,u,(p+1)%6);
}
}
vector<int> solve(int M)
{
res.resize(M);
dfs(0,-1,0);
return res;
}
}
vector<int> Mark(int N,int M,int A,int B,vector<int> U,vector<int> V)
{
for(int i=0;i<M;i++)
{
e[U[i]].push_back(make_pair(V[i],i));
e[V[i]].push_back(make_pair(U[i],i));
}
if(A>=3)
{
queue<int> q;
vector<int> res(M);
memset(dis,-1,sizeof(dis));
q.push(0);
dis[0]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
for(auto E:e[u])
{
int v=E.first;
if(dis[v]==-1)
{
dis[v]=dis[u]+1;
q.push(v);
}
}
}
for(int i=0;i<M;i++)
res[i]=min(dis[U[i]],dis[V[i]])%3;
return res;
}
else return col01::solve(M);
}
Catherine.cpp:
#include "Catherine.h"
#include <iostream>
using namespace std;
int a,b,lastc,fir,movec;
bool known,sta;
vector<int> step;
void Init(int A,int B)
{
a=A,b=B;
}
int Move(vector<int> y)
{
if(a>=3)//subtask 1-4
{
int p=-1,q=-1;
for(int i=0;i<3;i++)
if(y[i])p==-1?p=i:q=i;
if(p!=-1&&q==-1)return p;
return (p==0&&q==2)?2:p;
}
else//subtask 5-7
{
int cnt=0;
for(auto x:y)
cnt+=x;
if(cnt+sta>=3)//point with >=3 degrees
{
known=true;
if(!sta)
{
sta=true;
return lastc=(y[1]==1);
}
if(!y[lastc])return -1;
y[lastc]++;
return lastc=(y[1]==1);
}
else if(cnt==1-sta)//get into leaf point
{
known=true;
if(!sta)
{
sta=true;
return lastc=(y[1]==1);
}
return -1;
}
else//2 degree point
{
sta=true;
if(known)//only one choice
return lastc=(y[1]==1);
else
{
if(step.size()==0)//first step
{
if(y[0]==2)//00
{
fir=1,step.push_back(0);
return lastc=0;
}
else if(y[1]==2)//11
{
fir=2,step.push_back(1);
return lastc=1;
}
else //01
{
fir=3,step.push_back(0);
return lastc=0;
}
}
else if(step.size()==1)//second step
{
if(fir==1)//00
{
step.push_back(1);
return lastc=1;
}
else if(fir==2)//11
{
step.push_back(0);
return lastc=0;
}
else//01
{
if(y[1])
{
step.push_back(1);
return lastc=1;
}
else
{
step.push_back(0);
return lastc=0;
}
}
}
else if(step.size()==2)//third step
{
if(fir==1||fir==2)//00 or 11
{
known=true;
if(y[0])//right way
return lastc=0;
else//wrong way
return -1;
}
else//01
{
if(step[1]==0)
{
step.push_back(1);
return lastc=1;
}
else
{
known=true;
if(y[1])//right way
return lastc=1;
else//wrong way
return -1;
}
}
}
else//last step,01 only
{
known=true;
if(y[0])//right way
return lastc=0;
else
return -1;
}
}
}
}
}