这次 NOI Online 入门组考了一道裸的整数拆分问题。
SF 实在太菜,只会暴力,不会这题的正解。
这个菜鸡决定查些资料,好好研究一下整数拆分问题背后的那些事情。
Warning:阅读本文需要一些生成函数与形式幂级数的相关知识,如果您还不了解的话,推荐先阅读 铃悬的数学小讲堂——生成函数初步。
1 五边形数
五边形数(Pentagonal number)\(p_n\) 大概长这个样子:
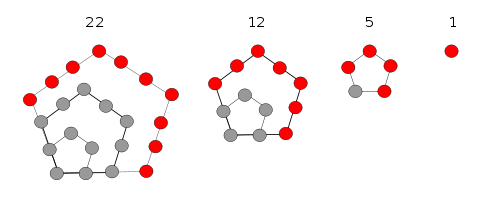
简单来说,大概就是一个边长 \(n\)(指边上有 \(n\) 个点)的五边形,里面套一个边长 \(n-1\) 的五边形,以此类推。
从图中很容易看出递推式:\(p_n=p_{n-1}+3n-2\),边界是 \(p_1=1\)(其实 \(n=1\) 时上述递推式仍然成立,不过考虑它的几何意义还是将 \(n=1\) 当作边界)。
根据这个递推式,很容易得出它的通项式:
$$
\begin{align}
p_n &= p_{n-1}+3n-2\\
&= p_{n-2}+3(n-1)-2+3n-2\\
&= \ldots\\
&= \sum_{i=1}^{n} 3i-2\\
&= \frac{3n^2-n}{2}
\end{align}
$$
五边形数在 OEIS 上的编号是 A000326。
五边形数的性质很多,这里简单列出几条:
- 任何正整数都可以表示为不超过 \(5\) 个五边形数的和(详见 费马多边形数定理)。事实上绝大多数正整数都可以拆分为 \(3\) 个五边形数的和。
- 前 \(n\) 个五边形数的平均数是第 \(n\) 个三角形数。
2 广义五边形数
上面的式子中 \(n\) 的取值是正整数,如果将 \(n\) 的取值范围扩大到全体整数,会不会仍然具有一些优雅的性质呢?
于是我们按照 \(n=0,1,-1,2,-2,3,-3,4,-4,\ldots\) 的顺序代入上面的通项式,得到下面的数列:
$$
0, 1, 2, 5, 7, 12, 15, 22, 26,\ldots
$$
这个数列是在原来五边形数的基础上扩充范围得到的,于是我们称其为广义五边形数。它在 OEIS 上的编号为 A001318。
为了方便,广义五边形数仍然用 \(p_n\) 表示。
广义五边形数和下面要讲到的整数拆分问题有很大联系,我们在下文将会深入探究。
3 五边形数定理
介绍一个新函数:欧拉函数。
(注意:这里的欧拉函数 \(\phi(x)\) 不是数论里的那个欧拉函数 \(\varphi(x)\))
$$
\phi(x)=\prod_{k=1}^{\infty}(1-x^k)
$$
将这个式子展开(这个展开首先由欧拉完成):
$$
\prod_{k=1}^{\infty}(1-x^k)=\sum_{k=-\infty}^{\infty}(-1)^k x^{\frac{3k^2-k}{2}}
$$
注意 \(x\) 的次数,正是我们前面提到的广义五边形数。五边形数定理由此得名。
将得到的所有项按升幂排列,得到:
$$
\phi(x)=1-x-x^2+x^5+x^7-x^{12}-x^{15}+\ldots
$$
这个展开式的证明太神仙了,笔者并不会,感兴趣的可以看 visit_world 大爷的博客。
得到这个式子有什么用呢?它和我们接下来要提到的整数拆分问题有很大关系。
4 整数拆分问题
接下来进入重头戏。
我们来回顾一下刚刚结束的 NOI Online 里考到的 这道题:
求将正整数 \(n\) 拆分为若干个正整数的和(允许同一个数使用多次,这里的拆分是无序的,即 \(1+2\) 和 \(2+1\) 等价)的方案数。
本题有很多做法,时间效率不尽相同。下面介绍一种运用生成函数的方法。
下面设 \(p(x)\) 为拆分 \(x\) 的方案数(\(p(x)\) 在 OEIS 上的编号为 A000041)。
考虑 \(p(x)\) 的生成函数,
$$
\sum_{k=0}^{\infty}p(k)x^k=\prod_{k=1}^{\infty}\frac{1}{1-x^k}=\frac{1}{\phi(x)}
$$
用五边形数定理展开一下,整理下式子:
$$
\begin{aligned}
\phi(x)\sum_{k=0}^{\infty}p(k)x^k &= (1-x-x^2+x^5+x^7-\ldots)(1+p(1)x+p(2)x^2+p(3)x^3+\ldots)\\
&= 1
\end{aligned}
$$
现在我们想要求出 \(p(k)\),或者说,算出 \(x^k\) 前面的系数。
将整个式子展开,得到(展开过程这里略去,感兴趣的读者这里可以自己尝试):
$$
p(k)-p(k-1)-p(k-2)+p(k-5)+p(k-7)-\ldots=0
$$
(PS:有的人可能对这个过程有点疑惑,这里稍微讲一下。上面的等式成立,意味着 \(x^k\) 的系数(别忘了这里是形式幂级数)在左右两边是相等的。这个等式的左边是上面的式子展开后 \(x^k\) 的系数,右边因为只有常数,所以 \(x^k\) 的系数为零)
广义五边形数再一次出现在我们的式子里了。
根据上面这个式子,我们就可以递推计算 \(p(x)\) 的值了。
因为广义五边形数是 \(O(n^2)\) 的级别(不知道的,请翻到最上面看通项式),因此递推式共有 \(O(\sqrt n)\) 项,这样计算的时间复杂度便是 \(O(n \sqrt n)\)。
嗯,代码实现挺短的:
#include <iostream>
using namespace std;
long long f[100005];
int a(int x)
{
return (3*x*x-x)/2;
}
int main()
{
int n,p;
cin>>n>>p;
f[0]=1;
for(int i=1;i<=n;i++)
for(int j=1;;j++)
{
int x=a(j),y=a(-j);
if(x<=i)
f[i]=((f[i]+(j&1?1:-1)*f[i-x])%p+p)%p;
if(y<=i)
f[i]=((f[i]+(j&1?1:-1)*f[i-y])%p+p)%p;
if(x>i||y>i)break;
}
cout<<f[n]<<endl;
return 0;
}