又是一个新坑.jpg
一些记号
为了简单起见,下文采用了一些简便的记号,先在这里进行声明。
- \(A_{l \ldots r}\):表示 \(A_l, A_l+1, \ldots, A_r\) 这个子序列。
- \(sum_{l \ldots r}\):表示 \(\sum_{i=l}^r A_i\),简单来说是 \(A_{l \ldots r}\) 的区间和。
- \(pre_{l \ldots r}\):表示 \(\max_{i=l}^r \sum_{j=l}^i A_j\),简单来说是 \(A_{l \ldots r}\) 的最大前缀和。
- \(post_{l \ldots r}\):表示 \(\max_{i=l}^r \sum_{j=i}^r A_j\),简单来说是 \(A_{l \ldots r}\) 的最大后缀和。
- \(ans_{l \ldots r}\):表示 \(\max_{l \leq i \leq r,i \leq j \leq r} \sum_{k=i}^j A_k\),简单来说是 \(A_{l \ldots r}\) 的最大子段和。
如无特殊说明,最大前缀,最大后缀,最大子段均不为空。
GSS1
题目链接
https://www.spoj.com/problems/GSS1/
题意
给一个序列 \(A\) 和 \(q\) 个询问,每个询问求子序列 \(A_{l_i \ldots r_i}\) 的最大子段和 \(ans_{l \ldots r}\)。
题解
设法将这个问题拆分成子问题分治解决。
假如我们将一个子序列 \(A_{l \ldots r}\) 拆分成了两个子序列 \(A_{l \ldots x}\) 和 \(A_{x+1 \ldots r}\),如何把这两个子序列的信息合并,从而求出我们待求的 \(A_{l \ldots r}\) 的最大子段和呢?
简单地分类讨论下,我们发现 \(A_{l \ldots r}\) 的最大子段和 \(ans_{l \ldots r}\) 只可能是这三种情况:
- 最大子段只在左子序列;
- 最大子段只在右子序列;
- 最大子段跨越左右两个子序列。
如果是第一种情况,最大子段和显然是 \(ans_{l \ldots x}\);如果是第二种情况,最大子段和显然是 \(ans_{x+1 \ldots r}\)。这两种情况都很平凡。
我们重点关注一下第三类情况。
画个图就会发现,这种情况下,这个子段一定由左子序列的一个后缀和右子序列的一个前缀拼接而成。
因为左右子序列相互独立,我们的目标就是让左子序列的后缀和最大,右子序列的前缀和最大。也就是说,这种情况下的最大子段和为 \(post_{l \ldots x}+pre_{x+1 \ldots r}\)。
现在问题变成了如何求最大后缀和,最大前缀和。
还是采用分治的思想。
一个子序列 \(A_{l \ldots r}\) 的最大前缀和有且只有如下两种情况:
- 最大前缀右端点在左子序列内。
- 最大前缀右端点在右子序列内。
对于第一种情况,最大前缀和显然是 \(pre_{l \ldots x}\)。
对于第二种情况,这个最大前缀包含了整个左子序列和右子序列的一个前缀,也就是说,最大前缀和为 \(sum_{l \ldots x}+pre_{x+1 \ldots r}\)。
最大后缀和和最大前缀和同理,这里不再赘述。
最后的问题是,这个分治过程该怎样实现呢?
对于这样的区间问题,用线段树维护这些信息当然是最好的选择。
#include <iostream>
using namespace std;
struct seg
{
int ans,sum,pre,post;
seg operator+(const seg&a)const
{
seg res;
res.sum=sum+a.sum;
res.ans=max(ans,max(a.ans,post+a.pre));
res.pre=max(pre,sum+a.pre);
res.post=max(a.post,a.sum+post);
return res;
}
}s[200005];
int a[50005];
void pushup(int root)
{
s[root]=s[root<<1]+s[root<<1|1];
}
void build(int root,int l,int r)
{
if(l==r)
{
s[root]={a[l],a[l],a[l],a[l]};
return;
}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
seg query(int root,int cl,int cr,int l,int r)
{
if(l<=cl&&cr<=r)return s[root];
int mid=(cl+cr)>>1;
if(l<=mid&&mid<r)
return query(root<<1,cl,mid,l,r)+query(root<<1|1,mid+1,cr,l,r);
else if(l<=mid)
return query(root<<1,cl,mid,l,r);
else
return query(root<<1|1,mid+1,cr,l,r);
}
int main()
{
ios::sync_with_stdio(false);
int n,m;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
cin>>m;
while(m--)
{
int x,y;
cin>>x>>y;
cout<<query(1,1,n,x,y).ans<<endl;
}
return 0;
}
GSS2
(暂时咕了)
GSS3
题目链接
https://www.spoj.com/problems/GSS3/
题意
在 GSS1 的基础上加了个单点修改的操作。
题解
单点修改没有什么特别之处,只需在单点修改后更新相应信息即可。
#include <iostream>
using namespace std;
struct seg
{
int ans,sum,pre,post;
seg operator+(const seg&a)const
{
seg res;
res.sum=sum+a.sum;
res.ans=max(ans,max(a.ans,post+a.pre));
res.pre=max(pre,sum+a.pre);
res.post=max(a.post,a.sum+post);
return res;
}
}s[200005];
int a[50005];
void pushup(int root)
{
s[root]=s[root<<1]+s[root<<1|1];
}
void build(int root,int l,int r)
{
if(l==r)
{
s[root]={a[l],a[l],a[l],a[l]};
return;
}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
seg query(int root,int cl,int cr,int l,int r)
{
if(l<=cl&&cr<=r)return s[root];
int mid=(cl+cr)>>1;
if(l<=mid&&mid<r)
return query(root<<1,cl,mid,l,r)+query(root<<1|1,mid+1,cr,l,r);
else if(l<=mid)
return query(root<<1,cl,mid,l,r);
else
return query(root<<1|1,mid+1,cr,l,r);
}
void update(int root,int cl,int cr,int pos,int x)
{
if(cr<pos||pos<cl)return;
if(cl==cr)
{
s[root]={x,x,x,x};
return;
}
int mid=(cl+cr)>>1;
update(root<<1,cl,mid,pos,x);
update(root<<1|1,mid+1,cr,pos,x);
pushup(root);
}
int main()
{
ios::sync_with_stdio(false);
int n,m;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
cin>>m;
while(m--)
{
int op,x,y;
cin>>op>>x>>y;
if(op==0)update(1,1,n,x,y);
if(op==1)cout<<query(1,1,n,x,y).ans<<endl;
}
return 0;
}
GSS4
题目链接
https://www.spoj.com/problems/GSS4/
题意
给一个序列 \(A\),有两种操作:
- 对子序列 \(A_{l_{i} \ldots r_{i}}\) 中的每个数执行开平方下取整操作。
- 求 \(sum_{l_{i} \ldots r_{i}}\)。
题解
(详细题解请点 这里)
开方操作可以暴力执行,同时维护区间最大值,对区间最大值为 \(1\) 的区间就可以不用开方了(不会改变结果)。
一个数最多开方 \(6\) 次就会变成 \(1\),所以实际效率很高。
#include <cmath>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
struct seg
{
long long sum,maxa;
}s[400005];
long long a[100005];
void pushup(int root)
{
s[root].sum=s[root<<1].sum+s[root<<1|1].sum;
s[root].maxa=max(s[root<<1].maxa,s[root<<1|1].maxa);
}
void build(int root,int l,int r)
{
if(l==r)
{
s[root].sum=s[root].maxa=a[l];
return;
}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
void update(int root,int cl,int cr,int l,int r)
{
if(r<cl||cr<l)return;
if(s[root].maxa==1)return;
if(cl==cr)
{
s[root].sum=s[root].maxa=sqrt(s[root].sum);
return;
}
int mid=(cl+cr)>>1;
update(root<<1,cl,mid,l,r);
update(root<<1|1,mid+1,cr,l,r);
pushup(root);
}
long long query(int root,int cl,int cr,int l,int r)
{
if(r<cl||cr<l)return 0;
if(l<=cl&&cr<=r)return s[root].sum;
int mid=(cl+cr)>>1;
return query(root<<1,cl,mid,l,r)+query(root<<1|1,mid+1,cr,l,r);
}
int main()
{
ios::sync_with_stdio(false);
int n,kase=0;
while(cin>>n)
{
cout<<"Case #"<<++kase<<":"<<endl;
memset(s,0,sizeof(s));
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
int m;
cin>>m;
while(m--)
{
int op,x,y;
cin>>op>>x>>y;
if(x>y)swap(x,y);
if(!op)update(1,1,n,x,y);
else cout<<query(1,1,n,x,y)<<endl;
}
cout<<endl;
}
return 0;
}
GSS5
题目链接
https://www.spoj.com/problems/GSS5/
大意
给定一个序列 \(A\),\(q\) 次询问。
每次给出 \(x_1,y_1,x_2,y_2\),求:
$$\max_{x_1 \leq i \leq y_1,x_2 \leq j \leq y_2,i \leq j} ans_{i \ldots j}$$
保证 \(x_1 \leq x_2\),\(y_1 \leq y_2\)。但不保证左端点所在区间和右端点所在区间不相交。
题解
分两种情况讨论:
- 左端点和右端点所在区间不相交。
- 左端点和右端点所在区间相交。
对于第一种情况,我们结合一下图来理解:
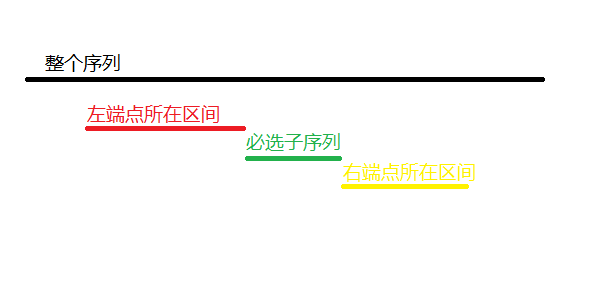
两个区间不相交的话,位于两个区间中间的子序列就变成了必选(满足条件的任何区间都包含这个子序列)。
需要注意的是,图上画的序列是连续的,但实际情况是离散的。因此需要注意区间端点的边界问题。
下面的部分涉及到边界问题的都会特别说明。
对于上面这种情况:答案就是左端点所在区间的最大后缀和,必选子序列的区间和,右端点所在区间的最大前缀和。
而且需要注意的是,这里的最大后缀和最大前缀都可以为空(接下来的讨论也一样)。
写成式子的形式是(注意边界问题):
$$post_{x_1 \ldots y_1-1}+sum_{y_1 \ldots x_2}+pre_{x_2+1 \ldots y_2}$$
第二种情况稍微复杂些,我们画一个图:
(这里放图)
从图上可以看出,一共有四种情况:
- 左端点,右端点都在两个区间的交区间内。
- 左端点不在两个区间的交区间内,右端点在两个区间的交区间内。
- 左端点在两个区间的交区间内,右端点不在两个区间的交区间内。
- 左端点,右端点都不在两个区间的交区间内。
对于情况一,就回到了 GSS1,求的实际上是 \(ans_{x_2 \ldots y_1}\)。
对于情况二,可以从上图看出看出答案是 \(post_{x1 \ldots x_2-1}+pre_{x_2 \ldots y_1}\)。
情况三和情况二类似,不再赘述。
而最后一种情况,则又回到了两个区间不相交的问题。
这样我们就完美解决了本题。
最后强调一遍,注意边界问题,以及本题中涉及的最大前后缀均可以为空。
#include <iostream>
using namespace std;
struct seg
{
int ans,sum,pre,post;
seg operator+(const seg&a)const
{
seg res;
res.sum=sum+a.sum;
res.ans=max(ans,max(a.ans,post+a.pre));
res.pre=max(pre,sum+a.pre);
res.post=max(a.post,a.sum+post);
return res;
}
}s[200005];
int a[50005];
void pushup(int root)
{
s[root]=s[root<<1]+s[root<<1|1];
}
void build(int root,int l,int r)
{
if(l==r)
{
s[root]={a[l],a[l],a[l],a[l]};
return;
}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
pushup(root);
}
seg query(int root,int cl,int cr,int l,int r)
{
if(l>r)return {0,0,0,0};
if(l<=cl&&cr<=r)return s[root];
int mid=(cl+cr)>>1;
if(l<=mid&&mid<r)
return query(root<<1,cl,mid,l,r)+query(root<<1|1,mid+1,cr,l,r);
else if(l<=mid)
return query(root<<1,cl,mid,l,r);
else
return query(root<<1|1,mid+1,cr,l,r);
}
int main()
{
ios::sync_with_stdio(false);
int t;
cin>>t;
while(t--)
{
int n,m;
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
cin>>m;
while(m--)
{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
if(y1<x2)
cout<<max(query(1,1,n,x1,y1-1).post,0)+query(1,1,n,y1,x2).sum+
max(query(1,1,n,x2+1,y2).pre,0)<<endl;
else
{
int ans1=query(1,1,n,x2,y1).ans;
int ans2=query(1,1,n,x1,x2-1).post+query(1,1,n,x2,y1).pre;
int ans3=query(1,1,n,x2,y1).post+query(1,1,n,y1+1,y2).pre;
int ans4=max(query(1,1,n,x1,x2-1).post,0)+query(1,1,n,x2,y1).sum+
max(query(1,1,n,y1+1,y2).pre,0);
cout<<max(ans1,max(ans2,max(ans3,ans4)))<<endl;
}
}
}
return 0;
}
GSS6
(平衡树,暂时咕了)
GSS7
题目链接
https://www.spoj.com/problems/GSS7/
题意
给出一棵树,树上每个点都有点权,有两种操作:
- 查询 \(a \to b\) 这条路径上的最大子段和(最大子段可以为空)。
- 将 \(a \to b\) 这条路径上的所有节点的点权改为 \(c\)。
题解
如果是序列问题的话,和 GSS3 几乎没啥区别(区间修改的话多写个 pushdown 就没了)。
然而这题很恶心地搬到了树上,多的不仅仅是树剖…
修改操作没啥好说的,重点是查询操作。
序列问题上的查询操作,由于遍历线段树时采用先序遍历,答案是自左向右一段段地合并,所以没有太大问题。
但树上的查询操作则是从两端(为了方便起见姑且叫左端和右端)开始,向中间合并,因此合并的顺序变得非常重要。
我们每次跳重链的时候,都要根据重链的归属(归属左边或是右边)将它的信息合并到相应的链上(一定要注意合并的方向是深度由深到浅)。
经过了几次跳重链的操作后,两个端点终于到了同一条重链。
现在我们拥有了两个链的信息,可以把它们直接合并来得到答案了吗?
并不是。左边的链方向是深度从深到浅,右边的链也是。我们需要反转其中一条链的方向,才能正确对接这两条链。
实现起来坑点真的不少…
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 1000000
using namespace std;
vector<int> e[100005];
int id[100005],siz[100005],son[100005],fa[100005],top[100005],dep[100005],cnt;
int x[100005],a[100005],n,q;
struct seg
{
int ans,sum,pre,post,tag;
seg operator+(const seg&a)const
{
seg res;
res.sum=sum+a.sum;
res.ans=max(ans,max(a.ans,post+a.pre));
res.pre=max(pre,sum+a.pre);
res.post=max(a.post,a.sum+post);
res.tag=0;
return res;
}
}s[400005];
void dfs1(int u,int f)
{
fa[u]=f;
dep[u]=dep[f]+1;
siz[u]=1;
for(auto v:e[u])
if(v!=f)
{
dfs1(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])
son[u]=v;
}
}
void dfs2(int u,int t)
{
top[u]=t;
id[u]=++cnt;
a[cnt]=x[u];
if(son[u])dfs2(son[u],t);
for(auto v:e[u])
if(v!=son[u]&&v!=fa[u])dfs2(v,v);
}
void pushup(int root)
{
int tag=s[root].tag;
s[root]=s[root<<1]+s[root<<1|1];
s[root].tag=tag;
}
void pushdown(int root,int l,int r)
{
if(s[root].tag!=INF)
{
int mid=(l+r)>>1,x=s[root].tag,ls=root<<1,rs=root<<1|1;
s[ls].tag=s[rs].tag=x;
s[ls].sum=(mid-l+1)*x;
s[ls].pre=s[ls].post=s[ls].ans=max((mid-l+1)*x,0);
s[rs].sum=(r-mid)*x;
s[rs].pre=s[rs].post=s[rs].ans=max((r-mid)*x,0);
s[root].tag=INF;
}
}
void build(int root,int l,int r)
{
if(l==r)
{
if(a[l]>=0)s[root]={a[l],a[l],a[l],a[l],INF};
else s[root]={0,a[l],0,0,INF};
return;
}
int mid=(l+r)>>1;
build(root<<1,l,mid);
build(root<<1|1,mid+1,r);
s[root].tag=INF;
pushup(root);
}
seg query(int root,int cl,int cr,int l,int r)
{
if(l<=cl&&cr<=r)return s[root];
pushdown(root,cl,cr);
int mid=(cl+cr)>>1;
if(l<=mid&&mid<r)
return query(root<<1,cl,mid,l,r)+query(root<<1|1,mid+1,cr,l,r);
else if(l<=mid)
return query(root<<1,cl,mid,l,r);
else
return query(root<<1|1,mid+1,cr,l,r);
}
void update(int root,int cl,int cr,int l,int r,int x)
{
if(r<cl||cr<l)return;
if(l<=cl&&cr<=r)
{
s[root].sum=(cr-cl+1)*x;
s[root].tag=x;
s[root].pre=s[root].post=s[root].ans=max(0,(cr-cl+1)*x);
return;
}
pushdown(root,cl,cr);
int mid=(cl+cr)>>1;
update(root<<1,cl,mid,l,r,x);
update(root<<1|1,mid+1,cr,l,r,x);
pushup(root);
}
seg query_chain(int x,int y)
{
seg lans={0,0,0,0,0},rans={0,0,0,0,0};
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])
{
rans=query(1,1,n,id[top[y]],id[y])+rans;
y=fa[top[y]];
}
else
{
lans=query(1,1,n,id[top[x]],id[x])+lans;
x=fa[top[x]];
}
}
if(dep[x]<dep[y])
rans=query(1,1,n,id[x],id[y])+rans;
else
lans=query(1,1,n,id[y],id[x])+lans;
swap(lans.pre,lans.post);
return lans+rans;
}
void update_chain(int x,int y,int z)
{
while(top[x]!=top[y])
{
if(dep[top[x]]>dep[top[y]])swap(x,y);
update(1,1,n,id[top[y]],id[y],z);
y=fa[top[y]];
}
if(dep[x]>dep[y])swap(x,y);
update(1,1,n,id[x],id[y],z);
}
int main()
{
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++)
cin>>x[i];
for(int i=1;i<n;i++)
{
int u,v;
cin>>u>>v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
cin>>q;
while(q--)
{
int op;
cin>>op;
if(op==1)
{
int a,b;
cin>>a>>b;
cout<<query_chain(a,b).ans<<endl;
}
else
{
int a,b,c;
cin>>a>>b>>c;
update_chain(a,b,c);
}
}
return 0;
}
GSS8
(平衡树,暂时咕了)