Johnson 和 Floyd 一样,是一种能求出无负环图上任意两点间最短路径的算法。该算法在 1977 年由 Donald B. Johnson 提出。
Part 1 算法概述
任意两点间的最短路可以通过枚举起点,跑 \(n\) 次 Bellman-Ford 算法解决,时间复杂度是 \(O(n^2m)\) 的,也可以直接用 Floyd 算法解决,时间复杂度为 \(O(n^3)\)。
注意到堆优化的 Dijkstra 算法求单源最短路径的时间复杂度比 Bellman-Ford 更优,如果枚举起点,跑 \(n\) 次 Dijkstra 算法,就可以在 \(O(nm\log m)\) (本文中的 Dijkstra 采用 priority_queue 实现,下同)的时间复杂度内解决本问题,比上述跑 \(n\) 次 Bellman-Ford 算法的时间复杂度更优秀。
但 Dijkstra 算法不能正确求解带负权边的最短路,因此我们需要对原图上的边进行预处理,确保所有边的边权均非负。
一种容易想到的方法是给所有边的边权同时加上一个正数 \(x\),从而让所有边的边权均非负。如果新图上起点到终点的最短路经过了 \(k\) 条边,则将最短路减去 \(kx\) 即可得到实际最短路。
但这样的方法是错误的。考虑下图:
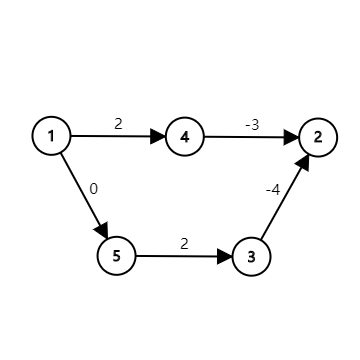
\(1 \to 2\) 的最短路为 \(1 \to 5 \to 3 \to 2\),长度为 \(-2\)。
但假如我们把每条边的边权加上 \(5\) 呢?
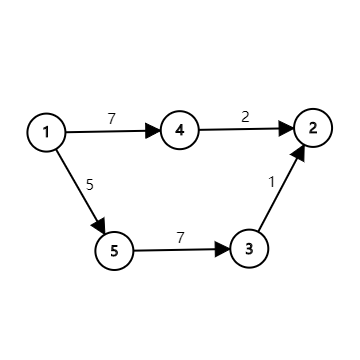
新图上 \(1 \to 2\) 的最短路为 \(1 \to 4 \to 2\),已经不是实际的最短路了。
Johnson 算法则通过另外一种方法来给每条边重新标注边权。
我们新建一个虚拟节点(在这里我们就设它的编号为 \(0\))。从这个点向其他所有点连一条边权为 \(0\) 的边。
接下来用 Bellman-Ford 算法求出从 \(0\) 号点到其他所有点的最短路,记为 \(h_i\)。
假如存在一条从 \(u\) 点到 \(v\) 点,边权为 \(w\) 的边,则我们将该边的边权重新设置为 \(w+h_u-h_v\)。
接下来以每个点为起点,跑 \(n\) 轮 Dijkstra 算法即可求出任意两点间的最短路了。
容易看出,该算法的时间复杂度是 \(O(nm\log m)\)。
Q:那这么说,Dijkstra 也可以求出负权图(无负环)的单源最短路径了?
A:没错。但是预处理要跑一遍 Bellman-Ford,还不如直接用 Bellman-Ford 呢。
Part 2 正确性证明
为什么这样重新标注边权的方式是正确的呢?
在讨论这个问题之前,我们先讨论一个物理概念——势能。
诸如重力势能,电势能这样的势能都有一个特点,势能的变化量只和起点和终点的相对位置有关,而与起点到终点所走的路径无关。
势能还有一个特点,势能的绝对值往往取决于设置的零势能点,但无论将零势能点设置在哪里,两点间势能的差值是一定的。
接下来回到正题。
在重新标记后的图上,从 \(s\) 点到 \(t\) 点的一条路径 \(s \to p_1 \to p_2 \to \ldots \to p_k \to t\) 的长度表达式如下:
$$(w(s,p_1)+h_s-h_{p_1})+(w(p_1,p_2)+h_{p_1}-h_{p_2})+ \ldots +(w(p_k,t)+h_{p_k}-h_t)$$
化简后得到:
$$w(s,p_1)+w(p_1,p_2)+ \ldots +w(p_k,t)+h_s-h_t$$
无论我们从 \(s\) 到 \(t\) 走的是哪一条路径,\(h_s-h_t\) 的值是不变的,这正与势能的性质相吻合!
为了方便,下面我们就把 \(h_i\) 称为 \(i\) 点的势能。
上面的新图中 \(s \to t\) 的最短路的长度表达式由两部分组成,前面的边权和为原图中 \(s \to t\) 的最短路,后面则是两点间的势能差。因为两点间势能的差为定值,因此原图上 \(s \to t\) 的最短路与新图上 \(s \to t\) 的最短路相对应。
到这里我们的正确性证明已经解决了一半——我们证明了重新标注边权后图上的最短路径仍然是原来的最短路径。接下来我们需要证明新图中所有边的边权非负,因为只有在非负权图上,Dijkstra 才能保证得出正确的结果。
根据三角形不等式,图上任意一边 \((u,v)\) 上两点满足:\(h_v \leq h_u + w(u,v)\)。这条边重新标记后的边权为 \(w'(u,v)=w(u,v)+h_u-h_v \geq 0\)。这样我们证明了新图上的边权均非负。
至此,我们就证明了 Johnson 算法的正确性。
Part 3 参考代码
#include <cstdio>
#include <cstring>
#include <queue>
#define INF 0x3f3f3f3f
using namespace std;
struct edge
{
int v,w,next;
}e[10005];
struct node
{
int dis,id;
bool operator<(const node&a)const
{
return dis>a.dis;
}
node(int d,int x)
{
dis=d,id=x;
}
};
int head[5005],h[5005],vis[5005],dis[5005],cnt;
void addedge(int u,int v,int w)
{
e[++cnt].v=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt;
}
void spfa(int s)
{
queue<int> q;
memset(h,INF,sizeof(h));
h[s]=0,vis[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(h[v]>h[u]+e[i].w)
{
h[v]=h[u]+e[i].w;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
return;
}
void dijkstra(int s)
{
priority_queue<node> q;
memset(dis,INF,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
q.push(node(0,s));
while(!q.empty())
{
int u=q.top().id;
q.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
if(!vis[v])q.push(node(dis[v],v));
}
}
}
return;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
addedge(u,v,w);
}
for(int i=1;i<=n;i++)
addedge(0,i,0);
spfa(0);
/*
for(int i=1;i<=n;i++)
printf("%d ",h[i]);
puts("");
*/
for(int u=1;u<=n;u++)
for(int i=head[u];i;i=e[i].next)
e[i].w+=h[u]-h[e[i].v];
for(int i=1;i<=n;i++)
{
dijkstra(i);
/*
for(int j=1;j<=n;j++)
printf("%d ",dis[j]==INF?INF:dis[j]+h[j]-h[i]);
puts("");
*/
}
return 0;
}
Reference
- Johnson’s algorithm – Wikipedia
- 《算法导论(中译本,第 3 版)》,25.3 用于稀疏图的 Johnson 算法,409-411 页